4.4. Машинное обучение на примерах. Нейронные сети. ч.2

Нейрон получает на входе сигналы x1, x2, x3,…, xN. И суммирует их с весовыми коэффициентами w:

s = ∑wixi
Однако на выходе нейрона присутствует сигнал только тогда, когда s больше или меньше какого-то порога. Точнее существует некоторая функция активации y = f(s), которая преобразует s в 1 (есть сигнал) или 0 (нет сигнала). Если на выходе нейрона есть сигнал, то говорят, что данный нейрон возбужден.
Распространены такие функции активации [12]:
ступенчатая пороговая:
y =1 при f(s)>=w0, где w0 – некоторый порог;
y =0 при f(s) сигмоидная (логистическая):
у = (1+exp(-as))-1
а также ряд других, несколько менее распространенных функций активации [14]. На рисунке рисунке 4.2 показаны графики названных функций.



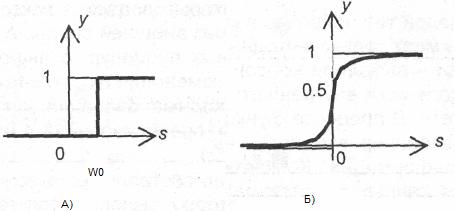
Рисунок 4.2 - Примеры функций активации:
А) - функция пороговая (единичного скачка);
Б) - сигмоидная (логистическая)



Коэффициенты w называются еще весами синаптических связей, т.к. в реальном биологическом нейроне соединения линий связи с телом нейрона происходит в точках, которые называются синапсами. При этом веса синаптических связей могут быть как положительными, так и отрицательными. В первом случае говорят о возбуждающих связях, во втором – о тормозящих.
Обратите внимание, что формула работы нейрона соответствует уравнению прямой линии в N-мерном пространстве.
Представим, что эта линия (при известных w) разделяет два образа, два класса объектов, каждый из которых описывается наборами параметров x1, x2, x3,…, xN. В случае двух координат x1, x2 это бы иллюстрировалось рисунком 4.3.
Если на входе нейрона появляется объект с конкретными значениями x1, x2, то при известных синаптических весах на выходе будет число s. А потом это число сравнивается с порогом в соответствии с активационной функцией. Если на выходе 1, то объект попадает в одну область от прямой линии на рисунке 4.3 (соответствует одному классу), если 0 – в другую область, т.е. соответствует другому классу.
Таким образом, решается задача распознавания класса объекта, который характеризуется значениями признаков x1, x2, x3,…, xN. Интересно, что при соединении нейронов между собой в более сложную структуру из нескольких уровней итоговая линия разделения образов может быть гораздо сложнее, чем прямая (см. рисунок 4.3, [13]). На рисунке 4.3 кружками справа показаны объекты, а стрелки от линий показывают область, где на выходе нейрона будет сигнал. Слева показаны структуры сети – от простой однослойной до многослойной. Видно, что в сложной многоуровневой сети возможно ограничивать образы весьма сложными линиями границ. Это иллюстрирует применимость сложной НС для распознавания образов со сложными границами в многомерном пространстве признаков.



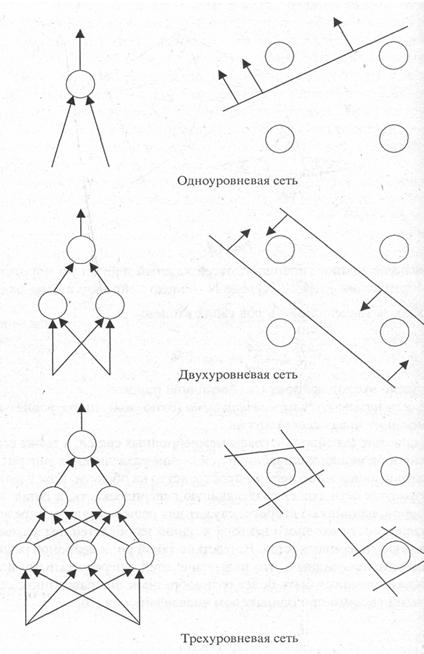
Рисунок 4.3 – Сложность структуры НС и границы распознаваемых образов



Рассмотрим более подробно структуру сети с одним слоем (рисунок 4.4). В ней выделяется один, так называемый, скрытый слой, один слой – входных нейронов, один слой – выходных.




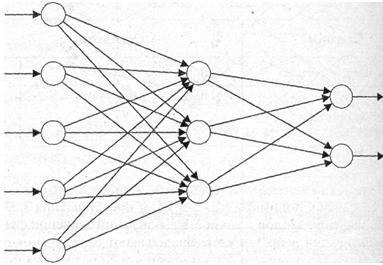
Рисунок 4.4. Нейронная сеть с одним скрытым слоем

Входные нейроны являются просто передатчиками входных сигналов x на второй – «думающий» слой нейронов. Число входных нейронов зависит от того, как кодируется описания объекта. Так, если графический символ представляется матрицей 8х8, то входных нейронов будет 64. При этом на каждом из них будет или сигнал 1 (то есть в данной клетке матрицы присутствует элемент символа), или – 0 (сигнал в клетке матрицы отсутствует).
Выходных нейронов столько, сколько образов система должна распознавать. Так, на рисунке 4.4. на выходе два нейрона для распознавания классов «А» и «Б». Возбуждение верхнего из них означает, что на входе сети объект класса «А», а возбуждение нижнего – объект класса «Б».
Модель сети, изображенная на рисунке 4.4 является моделью того самого однослойного перцептрона, который был предложен Ф. Розенблаттом. Многослойные персептроны (в которых более одного слоя скрытых элементов) были предложены и исследованы в 1960-х годах Ф.Розенблаттом, М.Минским, Д.Пейпертом и др. Сегодня существуют различные модели НС, отличные от той, что приведена на рисунке 4.4. В одной мо¬дели (т.е. для одного типа сетей) каждый элемент может быть связан со все¬ми другими элементами сети, в другой модели элементы могут быть органи¬зованы в некоторой упорядоченной по уровням (слоям) иерархии, где связи допускаются только между элементами в смежных слоях, а в третьей — могут допускаться обратные связи между смежными слоями или внутри одного слоя, или же допускаться посылка сигналов элементами самим себе. Воз¬можности здесь практически бесконечны, но обычно для каждой конкретной модели сети указывается тип допустимых связей [12].
Принципиально важным является вопрос обучения НС. Выше мы говорили, что для при распознавании, по сути, определяется положение объекта относительно линии (множества линий), разделяющей образы (рисунок 4.3). А линии эти задаются как раз числом связанных нейронов и синаптическими весами связей w.
Задачей обучения как раз и является - определить эти веса и структуру связей. Как это сделать? Можно пойти методом проб и ошибок – предъявлять на вход нейрона разные объекты и так поворачивать линию границы, чтобы все объекты попадали в тот класс, которому они и принадлежат (мы помним, что речь идет об обучении с учителем, когда нам известно, какой результат должен быть на выходе сети). Но такая стратегия подбора коэффициентов w довольно груба и может быть действенна только для простых сетей. Отсутствие эффективного алгоритма обучения для многослойных сетей было той важной теоретической проблемой, которая сдерживала развитие нейросетевого подхода на протяжении нескольких десятилетий. Простые правила обучения распространялись на однослйный персептроны. Лишь в середине 1980-х несколькими исследователями независимо друг от друга был предложен эффективный алгоритм обучения многослойных персептронов, основанный на вычислении градиента функции ошибки. Алгоритм был назван "обратным распространением ошибки" - back propagation [12].
В этом алгоритме на вход сети подается выборка обучающих примеров – объектов с разными характеристиками x1, x2, x3,…, xN. Для каждого объекта известна правильная реакция сети, т.е. известен выходной вектор (y1, y2,…, xM), где M – число выходных нейронов. Сравнивается фактический выход сети с ожидаемым и на это основе послойно вычисляются ошибки всех нейронов, а потом по этим ошибкам вводится корректировка весов.
Общая схема алгоритма состоит из следующих этапов [12,1]:
1) Инициализация сети. Весам сети присваиваются малые случайные значения.
2) Подача на вход обучающего примера, т.е. вектора данных для i-го (здесь- первого) образца (x1i, x2 i, x3 i,…, xN i).
3) Последовательно проходя по всем внутренним нейронам и связям между ними вычислить фактическую реакцию сети на выходных нейронах на этот i-й образец (y1* i, y2* i,…, xM* i).
4) По специальному правилу вычисляется отклонение - ошибка каждого выходного нейрона путем сравнения фактического (y1* i, y2* i,…, xM* i) и ожидаемого (y1, y2,…, xM).
5) На основе найденного отклонения по своим формулам вычисляется ошибка последнего скрытого слоя. Далее по этому значению вычисляется отклонение предпоследнего слоя и т.д.
6) На основе найденных отклонений вычисляется поправка в весовые коэффициенты синаптических связей для каждого элемента.
Далее все повторяется с новым обучающим образцом. Обучение заканчивается с окончанием обучающей выборки или в том случае, если ошибки сети становятся минимальны, т.е. далее не уменьшаются.

Читать дальше:

4.4. Машинное обучение на примерах. Нейронные сети. ч.3