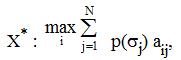4.5. Принятие решений в условиях риска и неопределенности

4.5. Принятие решений в условиях риска и неопределенности

Выше мы рассматривали принятие решений с учетом оценки полезности альтернатив. Во многих практических задачах полезность альтернативы или отдельные оценки по тем или иным показателям будут зависеть от некоторых условий, в которых принятое решение реализуется. Так, выбирая тот или иной план выпуска продукции по критерию максимизации прибыли ЛПР рассчитывает на некоторое состояние спроса, а также другие условия, которые вместе создают определенную ситуацию, в которой будет реализовываться решение. Изменение этих условий может привести к результатам, которые в корне отличаются от ожидаемых.

Говорят, что каждому решению соответствует некоторый исход. Исход определяется парой «альтернатива – условия реализации (ситуация)». Если возможны разные исходы и известны вероятности их возникновения, то говорят о задаче принятия решений в условиях риска; если вероятности исходов неизвестны, то говорят о задаче принятия решения в условиях неопределенности.

Задачи принятия решений в условиях риска и неопределенности можно интерпретировать как игру двух игроков, одним из которых является ЛПР, вторым – «природа». Первый игрок предпринимает шаги, т.е. выбирает альтернативы; второй игрок, «природа», ведет себя безразлично к действиям первого, но может находиться в одном из нескольких состояний (эти состояния и моделируют те ситуации, которые будут сопровождать реализацию альтернатив). Первый игрок должен так выбирать альтернативы, чтобы максимизировать свой выигрыш, который является в общем случае функцией двух переменных – альтернативы и состояния «природы».

Мощным инструментом решения подобных задач является интенсивно развивающаяся в последние десятилетия научная дисциплина - теория игр. В играх с природой при принятии решения ЛПР обладает следующей информацией:

- набор возможных состояний природы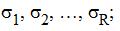

- множество Х возможных действий игрока –ЛПР, которые есть альтернативы. В терминах теории игр такие возможные действия игрока называются стратегиями;

- множество исходов и оценки исходов aij, где i – индекс альтернативы, j - индекс состояния природы. Исход i-й альтернативы с его оценкой зависит от j-го состояния природы.

В ЗПР в условиях риска имеется еще информация о распределении вероятностей состояний «природы» p(sj).

Имеющаяся информация фиксируется с помощью специальных таблиц, которые называются матрицами игры. В таблице на пересечении строк и столбцов устанавливаются оценки исходов. Эти оценки также как и ранее могут быть измерены в разных шкалах (относительной, абсолютной, балльной). Пример матрицы игры показан в табл.4.2, где предполагается, что оценки исходов получены в относительной шкале.

В теории игр основным критерием выбора является критерий максимина (этот критерий есть, по существу, известный нам уже критерий Вальда):





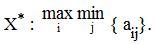
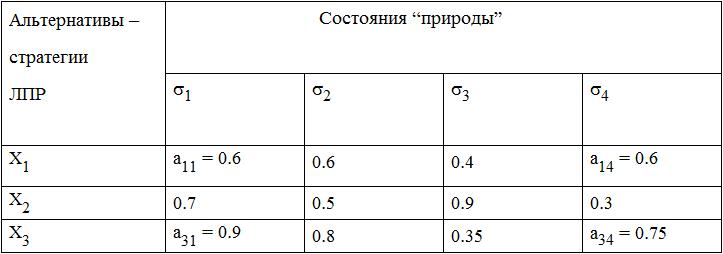
Таблица 4.2.

Матрица игры (для иллюстрации ЗПР в условиях неопределенности)




В теории игр основным критерием выбора является критерий максимина (этот критерий есть, по существу, известный нам уже критерий Вальда):



Он предполагает выбор той альтернативы, которая в самом неблагоприятном случае даст оценку исхода – выигрыш ЛПР больше, чем другие альтернативы. Выбор по этому критерию называют еще принятием решения в расчете на гарантированный результат. Так, по табличным данным альтернатива X1 даже в самом неблагоприятном случае обеспечит гарантированный выигрыш a13 = 0.4 (в то время, как другие альтернативы – только 0.3 или 0.35) и потому является лучшей для принятия решения в условиях неопределенности.

Кроме критерия максимина (критерия Вальда) применяется также критерий Гурвица (см. выше), согласно которому лучшей следует считать ту стратегию (альтернативу), которая приводит к наибольшему значению линейной свертки наихудшего и наилучшего для каждой стратегии результата.

В условиях риска известны вероятности состояний «природы» (и, соответственно, исходов). В этом случае может быть использован критерий выбора, который называется критерием математического ожидания (формально сходен с упомянутом выше критерием взвешенной суммы):




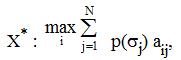
где выбирается та альтернатива X*, математическое ожидание выигрыша которой с учетом всех возможных состояний природы и вероятностей их возникновения является наибольшей.
 

Читать дальше:

#a href="http://www.systematy.ru/articles/46_ekspertiza_kak_metod_polucheniya_informatsii_v_zadachah_prinyatiya_resheniy"#4.6 Экспертиза как метод получения информации в задачах принятия решений#/a#