4.6 Экспертиза как метод получения информации в задачах принятия решений
4.6 Экспертиза как метод получения информации в задачах принятия решений
Во многих задачах системного анализа непосредственное измерение или расчет по формулам показателей для характеристики альтернатив невозможен или крайне затруднителен. Это, например, характерно для задач анализа, управления или совершенствования сложных организационно-экономических систем. Часто сам характер показателя такой, что предполагает не просто измерение, а выражение некоторого мнения специалиста. Например, сравнивая двух изготовителей продукции, из которых выбирается возможный поставщик, можно ввести общий показатель надежности поставщика. Оценку этому показателю может дать опытный специалист, хорошо знающий работу данного изготовителя. Высказывая свое мнение, этот специалист может использовать известные нам шкалы измерений (относительную, балльную, ранговую), а ЛПР, сравнивая полученные оценки может сделать обоснованный выбор поставщика по критерию его надежности.
В ЗПР таким специалистом, мнение которого может быть использовано для оценки характеристик альтернатив, является эксперт (см. данное выше определение). В приведенной выше постановке ЗПР и способах выбора альтернатив можно выделить следующие типовые задачи экспертного оценивания:
- оценка значения некоторого показателя f(Х) альтернативы Х;
- оценка коэффициентов значимости показателей ai в критерии взвешенного суммирования;
- упорядочение (ранжирование) показателей по важности;
- упорядочение (ранжирование) альтернатив по некоторому признаку, например, по их полезности для ЛПР;
- формирование множества показателей, по которым будет оцениваться альтернатива;
- формирование исходного множества альтернатив, из которых будет осуществляться выбор.
Ниже ознакомимся со способами решения таких задач, более глубокие сведения из области экспертного оценивания можно найти в приводимой литературе.
На рис. 4.2. показана общая схема организации и проведения экспертизы. При решении задач экспертного оценивания, чтобы субъективные мнения экспертов были приближены к объективным оценкам, привлекаются, как правило, несколько экспертов. Далее, мы увидим, что мнения разных экспертов также могут иметь разный вес. Это обусловлено возможно различной квалификацией экспертов в данной области проблем. Оценка значимости (веса) мнения эксперта может быть дана самостоятельно на основе специальной шкалы или в группе, когда один эксперт оценивает веса других.
Для самооценки (оценке в группе) эксперту можно предложить проставить себе балл (балл другому эксперту), используя следующую балльную шкалу:
10 баллов – эксперт специализируется по данному вопросу, имеет по нему успешно завершенные и используемые на практике разработки и практический опыт;
8 баллов – в решении проблем по данному вопросу эксперт не участвует, но этот вопрос входит в сферу его узкой специализации;
5 баллов – вопрос входит в сферу, тесно связанную с узкой специализацией эксперта, но в работе по данному вопросу он не участвует;
3 балла – вопрос не входит в сферу, тесно связанную с узкой специализацией эксперта.
Могут выставляться и промежуточные значения. Согласно данной шкале весовой коэффициент эксперта определяется путем деления полученной оценки на 10 баллов. Значения этих коэффициентов находятся в пределах от 0 до 1, их можно интерпретировать как вероятность верной оценки данным экспертом.
В случае оценки эксперта в группе вычисляется среднее арифметическое полученных весовых коэффициентов.
Рассмотрим способы решения некоторых задач.
Задача экспертного оценивания значения показателя. Пусть известен некоторый предлагаемый вариант действия – альтернатива X и известен показатель F, по которому требуется оценить альтернативу. Например, как и ранее это может быть оценка надежности предполагаемого поставщика. Пусть N экспертов дают собственные оценки надежности F(X)i по балльной шкале (например, по 10 балльной шкале). Требуется определить комбинированную экспертную оценку. Для вычисления комбинированной оценки используется следующая формула:
.gif)
Рис.4.2. Обобщенная схема экспертизы
.jpg) ,
,
где qi – весовой коэффициент i-го эксперта.
В более общем случае, когда qi необязательно принимает значения в пределах от 0 до1 и сумма весов всех экспертов неравна 1, формула становится такой:
.jpg)
Согласованность мнений экспертов может быть оценена по разбросу экспертных оценок:
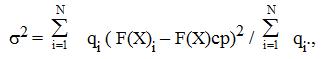
где F(X)ср – средняя арифметическая оценка.
Этот же способ комбинирования может быть использован при определении экспертным путем коэффициентов значимости показателей ai.
Задача ранжирования показателей (альтернатив). Пусть есть M показателей, необходимо упорядочить их по важности. Аналогично: есть множество альтернатив, необходимо упорядочить их по привлекательности для принятия решения. Решение задачи иллюстрируется с помощью табл.4.3. Здесь выбрано М=7, количество экспертов N = 5. Каждый эксперт проставляет свой ранг показателю (альтернативе), где ранг равный 1 означает наибольший приоритет показателя (альтернативы).
Сумма рангов уже позволяет упорядочить объекты экспертизы – так по данным табл. 4.3 можно получить следующую упорядоченную последовательность объектов (показателей, альтернатив):
5 – 3 – 2 – 1 – 6 – 4 - 7,
где 7-й объект оказался последним в списке, т.к. все эксперты единодушно присудили ему наивысший ранг. При необходимости, можно вычислить итоговый ранг, который рассчитывается как среднее арифметическое частных оценок.
В данном примере не учитываются весовые коэффициенты экспертов. Вычисление итогового ранга для упорядочения объектов с учетом весовых коэффициентов выполняется по формуле, аналогичной формуле комбинирования оценок в предыдущей задаче (предлагается сделать самостоятельно).
.jpg)
Таблица 4.3.
Данные для оценки согласованности мнений 5 экспертов при ранжировании показателей (альтернатив)
Важной характеристикой является согласованность мнений экспертов. Согласованность проверяется по величине коэффициента конкордации Кендалла:
W = 12 * S/[N2 * (M3 - M)],
где S – сумма квадратов отклонений всех оценок рангов каждого объекта экспертизы от среднего арифметического (см. табл.4.3.);
N - число экспертов;
M – число объектов экспертизы.
Коэффициент конкордации измеряется в диапазоне от 0 до1 , причем 0 соответствует полной несогласованности мнений, а 1 – полной согласованности. Если значение W превышает 0.4 - 0.5, то качество оценки считается удовлетворительной; если W 07.-0.8 – качество оценки считается высоким.
Определим степень согласованности мнений экспертов по данным табл.4.3. Среднее арифметическое число рангов
Rср = (21 + 15 + 9 + 28 + 7 + 25 + 35) = 20.
Затем оценим сумму квадратов отклонений от среднего: S = 630. Далее определим величину коэффициента конкордации:
W = 12* 630/25* (343-7) = 0.9.
Полученный результат свидетельствует о том, что мнения экспертов очень хорошо согласованны.
Задача формирования исходного множества альтернатив выбора (множества показателей для оценки альтернатив). Решение этой задачи позволяет сформировать и поэтапно уточнить с помощью экспертов множество возможных альтернатив, из которых будет делаться выбор. Эта же задача может быть полезной в случая, когда требуется определить множество показателей, по которым будет оцениваться альтернативы или любые другие объекты. Далее для упрощения будем говорить о множестве альтернатив.
Общий алгоритм формирования экспертным путем множества альтернатив следующий:
1) на первом шаге каждый i-й эксперт предлагает свое множество альтернатив Xi;
2) далее строится объединенное множество альтернатив:
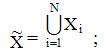
3) строится матрица R = (rij), где rij = 1, если j-я альтернатива i-го эксперта вошла в множество , т.е., если i-й эксперт предложил j-ю альтернативу; в противном случае rij = 0;
4) для каждой альтернативы определяется вероятность ее вхождения в искомое множество X по формуле:
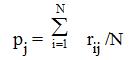
или, в случае разных весов экспертов,
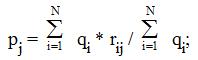
5) множество преобразуется в искомое множество альтернатив X. В искомое множество Х включаются те альтернативы, для которых pj не меньше, чем некоторый установленный порог pпор.
Для примера рассмотрим следующую задачу. Имеется фирма, занимающаяся внедрением корпоративных информационных систем на предприятиях. Работа эта достаточно сложная, трудоемкая и требует больших временных и финансовых затрат. Одним из первых этапов работ является проведение экспресс обследования и формирование общего представления о дальнейших этапах работы, на основе чего формируется техническое задание и заключается договор с предприятием - заказчиком. В крайнем случае по результатам экспресс обследования может быть принято решения и об отказе дальнейшего сотрудничества с предприятием.
Задачей экспертов является формирование множества тех показателей, по которым далее будет оценено предприятие и принято решения о дальнейших планах взаимодействия (следовательно, и вариантов технических заданий) или об отказе от работ. Пусть опрашиваются 3 эксперта. Предположим, что первый предложил включить в число показателей следующие:
- наличие на предприятии опыта использования автоматизированных систем управления, обозначим этот показатель как f1;
- наличие руководителя высокого ранга, активно заинтересованного во внедрении корпоративной системы, - f2;
- платежеспособность предприятия - f3.
Пусть второй эксперт кроме перечисленных показателей предложил включить в искомое множество также такой, как наличие на предприятии специалистов, имеющих опыт организации и администрирования компьютерных сетей - f4. Третий эксперт предложил рассматривать показатель f3, а также следующие показатели:
- удаленность предприятия от места жительства - f5;
- наличие симпатичного главного бухгалтера, который сможет войти в команду разработчиков в качестве консультанта - f6.
Таблица 4.4
Результаты формирования множества показателей
.jpg)
В табл. 4.4 приведены результаты опроса экспертов и результаты обработки экспертных мнений с помощью приведенного выше алгоритма.
Пусть установлен порог pпор.=2/3 (т.е. проходным является то мнение, с которым согласны две трети экспертов). Тогда в искомое множество показателей, по которым будет оцениваться потенциальный заказчик войдут показатели f1, f2, f3.
Читать дальше:
#a href=http://www.systematy.ru/articles/51_predmet_zadachi_sposobyi_i_priemyi_ekonomicheskogo_analiza#Предмет, задачи, способы и приемы экономического анализа #/a#
.gif)
.jpg) ,
,.jpg)
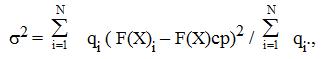
.jpg)
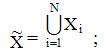
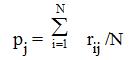
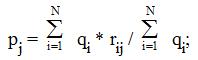
.jpg)