5.2. Методы анализа количественного влияния факторов на изменение показателей
5.2. Методы анализа количественного влияния факторов на изменение показателей
Общее определение показателя было дано в гл.2, а в гл.4 этот термин употреблялся для характеристики альтернатив. Показатели могут быть частными или, еще говорят, простыми, а также комплексными (агрегированными, сложными). Частные показатели характеризуют отдельные свойства объектов, процессов, они не вычисляются на основе других показателей. Комплексные показатели характеризуют интегрированные свойства объектов, процессов. Они вычисляются на основе других, более простых показателей.
В экономическом анализе используются следующие модели зависимости одних показателей от других (они называются факторными моделями, происхождение такого названия станет понятным несколько позже). Пусть F – комплексный показатель; f1, f2, f3 – частные показатели. Запишем факторные модели на примере этих показателей:
1. Аддитивная модель:
F = f1 + f2;
Кроме аддитивной модели можно говорить еще и о разностной модели – когда знак “+” заменяется на знак “-”.
2. Мультипликативная модель:
F = f1 * f2;
3. Кратная модель:
F = f1 /f2;
4. Смешанные (комбинированные) модели:
F = (f1 + f2) f3;
F = (f1 * f2) /f3;
F = (f1 + f2) / f3;
F = f1 /( f2 + f2).
Конечно, в формулах может быть и больше число показателей, чем два или три. Хотя в практических аналитических задачах их бывает не так много, что вызвано желанием упростить рассуждения. Это обеспечивается использованием многоступенчатого анализа, когда в правой части формулы также применяются комплексные, но более простые показатели. Их анализ проводится на другой ступени.
Если тот или иной показатель рассматривается как следствие, результат действия одной или нескольких причин, является объектом исследования, то при изучении взаимосвязей его называют результативным показателем. Показатели, определяющие поведение результативного (говорят еще - результатного, результирующего) показателя, называются факторными или просто – факторами. В приводимых выше формулах результатным является комплексный показатель F, факторами - f1, f2, f3.
В задачах анализа влияния факторов на изменение результативного показателя считаются известными следующие сведения: данные о значениях показателей в отчетный период и данные о значениях этих же показателей в базисный период. Под базисным понимается тот период, с которым сравниваем показатели отчетного. Показатели базисного периода мы будем обозначать с индексом Fб, показатели отчетного - Fо.
Характер задачи анализа влияния факторов покажем на следующем простом примере. Пусть в 1999 году на предприятии работало f1б = 100 рабочих, среднесуточная выработка продукции одним рабочим была f2б = 20 единиц и общий объем выработки в сутки в среднем составлял Fб = 2000 единиц. Через год, подводя итоги 2000г. руководство увидело, что общий объем суточной выработки увеличился и составил Fо = 5000 единиц, что даже превысило желаемый уровень. Среди общего ликования один из менеджеров предприятия задался вопросом, за счет какого из факторов и насколько произошло желаемое увеличение, а, значит, можно ли данный результат считать хорошим? Очевидно, что общий объем мог вырасти за счет увеличения производительности, и это – хорошо, но мог вырасти и за счет простого увеличения числа работающих, а отнесение такого результата к числу хороших – уже спорный вопрос. Были подняты учетные данные, которые дали следующие цифры: f1о = 200 рабочих, f2о = 25 единиц. И далее с помощью некоторых методов факторного анализа мы попробуем ответить на вопрос о количественном влиянии факторов на результирующий показатель в данной задаче.
Метод дифференциального исчисления. Теоретической основой для количественной оценки роли отдельных факторов в динамике результирующего показателя является дифференцирование.
В методе дифференциального исчисления предполагается, что общее приращение функций (результативного показателя) различается на слагаемые, где значение каждого из них определяется как произведение соответствующей частной производной на приращение переменной, по которой вычислена данная производная. Рассмотрим задачу нахождения влияния факторов на изменение результативного показателя методом дифференциального исчисления на примере функции от двух переменных.
Пусть задана функция z =f(x, у). Тогда, если функция дифференцируема, ее приращение можно выразить как
.jpg)
где Dz = zо - zб - изменение функции;
Dx = xо - xб – изменение первого фактора;
Dy = yо - yб – изменение второго фактора.
![]() - бесконечно малая величина более высокого порядка, чем
- бесконечно малая величина более высокого порядка, чем ![]() .
.
В методе принимается, что величиной ![]() можно пренебречь. Тогда влияние факторов х и у на изменение z определяется по формулам:
можно пренебречь. Тогда влияние факторов х и у на изменение z определяется по формулам:
.jpg)
где ![]() zх – изменение результативного показателя за счет фактора х;
zх – изменение результативного показателя за счет фактора х;
![]() zy – изменение результативного показателя за счет фактора y.
zy – изменение результативного показателя за счет фактора y.
Рассмотрим применение метода на примере конкретной функции, точнее на примере конкретной задачи, которая была сформулирована выше. В ней используется следующая факторная модель: F = f1 * f2.
Сведем исходные данные воедино:
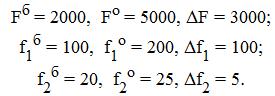
Найдем формулы для оценки влияния первого фактора:
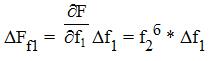
и, аналогично - второго фактора:
![]()
Подставляя в формулы известные данные, получим:
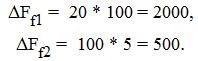
Таким образом, за счет увеличения производительности труда результативный показатель улучшился только на 500 единиц, в то время, как остальное увеличение в 2000 единиц произошло за счет простого роста числа рабочих. Учитывая, что каждому из вновь принятых нужно было платить зарплату, решать социальные вопросы, становится весьма сомнительным полученный итоговый результат увеличения выработки продукции.
Внимательный читатель увидит, что в нашей задаче сумма влияния факторов не дает общего приращения результативного показателя:
![]()
Правомерен вопрос: куда делся остальной прирост в 500 единиц и за счет какого фактора он произошел? Метод дифференцирования не дает ответа на этот вопрос. Дело в том, что отбрасываемое слагаемое – неразложимый остаток ![]() является действительно малой величиной только при малом изменении самих факторов. В противном случае в таких моделях, как, например, мультипликативная получаются достаточно большие погрешности в расчетах. Дальнейшие методы анализа пытаются тем или иным образом решить эту проблему.
является действительно малой величиной только при малом изменении самих факторов. В противном случае в таких моделях, как, например, мультипликативная получаются достаточно большие погрешности в расчетах. Дальнейшие методы анализа пытаются тем или иным образом решить эту проблему.
Метод простого прибавления неразложимого остатка. Не находя достаточно полного обоснования, что делать с остатком, в практике экономического анализа стали использовать прием прибавки неразложимого остатка к качественному или объемному (основному или производному) фактору, а также делить этот остаток между двумя факторами поровну. Качественным фактором считается, например, производительность труда, а объемным – количество рабочих.
Обозначим неразложимый остаток как d. Для рассмотренной выше двухфакторной мультипликативной модели справедливо:
![]()
Из этой формулы можно получить конечную формулу для двухфакторной мультипликативной модели (вывод предлагается сделать самостоятельно или посмотреть в [5]):
![]()
Если в эту формулу подставить численные значения из рассматриваемой задачи, то получим d = 100 * 5 = 500 – как раз столько, сколько было упущено при нахождении влияния факторов методом дифференцирования.
С учетом изложенного можно получить следующий набор рабочих формул в методе простого прибавления неразложимого остатка:
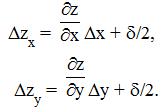
В задачах, где выделяются качественные и объемные факторы иногда весь неразложимый остаток относят на счет только одного качественного фактора.
Одним из наиболее универсальных методов анализа влияния факторов считается метод цепных подстановок. Он используется во всех типах факторных моделей. Общая идея метода заключается в следующем. сначала в формулу результатного показателя подставляются все значения факторов за базисный период. Потом значение одного фактора меняется на значение отчетного периода и вычисляется прирост, который эта подстановка обеспечит. Потом второй фактор также принимает значение из отчетного периода и вычисляется прирост, потом третий и т.д. общую последовательность подстановок можно проиллюстрировать следующим образом. Пусть используется следующая модель:
F = F (a, b, c, d),
где F – результативный показатель;
a, b, c, d – факторы;
Fб = F (aб, bб, cб, dб) – функция результативного показателя в базисный период;
Fo = F (ao, bo, co, do) – в отчетный период.
Будем последовательно подставлять в первую функцию факторы из второй:
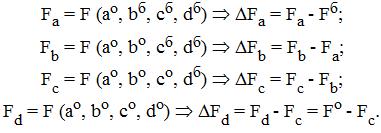
Проиллюстрируем применением метода на примере нашей задачи. Выполним первую подстановку:
Ff1 = f1о * f2б = 200 * 20 = 4000,
DF f1 = 4000 – 2000 = 2000.
После второй подстановки имеем:
Ff2 = f1о * f2о = 200 * 25 = 5000,
DF f2 = 5000 – 4000 = 1000.
Разницу с теми результатами, которые получены с помощью метода дифференцирования, предлагается оценить самостоятельно.
К сожалению, в данном методе результат будет существенно зависеть от порядка подстановки. Так, для нашей задач при ином порядке получим следующие результаты:
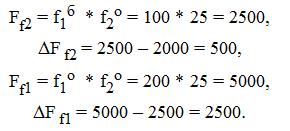
Как видно, изменение порядка привело к иному перераспределению все того же неразложимого остатка между факторами. В силу такой разницы результатов используя метод цепных подстановок необходимо придерживаться следующей последовательности расчетов: в первую очередь нужно учитывать изменение количественных (объемных), а затем качественных показателей. Другим подходом является использование следующей модификации данного метода.
Метод взвешенных конечных разностей состоит в том, что величина влияния каждого фактора определяется как по первому, так и по второму порядку подстановки, затем результат суммируется и от полученной суммы берется средняя величина, дающая единый ответ о значении влияния фактора. Если в расчете участвует больше факторов, то их значения рассчитываются по всем возможным подстановкам. Такое обилие числа всех возможных подстановок затрудняет использование метода в многофакторной модели.
Проиллюстрируем метод на примере сформулированной выше задаче об оценке факторов на объем выпуска продукции, используя результаты обоих вариантов подстановок. Номер подстановки в величине влияния фактора обозначим штрихом. В первой подстановке имеем

Итоговый результат оценки влияния факторов определим как среднее арифметическое:
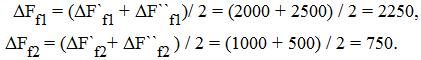
Таким образом, можно увидеть, что ![]() , т.е. неучтенный остаток устраняется. Отметим, что в общем случае для итоговой оценки вместо среднего арифметического применяется формула взвешенного суммирования, знакомая нам по гл.4.
, т.е. неучтенный остаток устраняется. Отметим, что в общем случае для итоговой оценки вместо среднего арифметического применяется формула взвешенного суммирования, знакомая нам по гл.4.
Кроме описанных выше существуют и другие методы факторного анализа. Достаточно распространены интегральный и логарифмический методы. Интегральный метод применяется для измерения влияния факторов в мультипликативных, кратных и кратно-аддитивных моделях. В этом методе для разных моделей и разного количества факторов используются рабочие формулы, которые получаются в результате специального математического вывода. С такими формулами использование интегрального метода не требует знания всего процесса интегрирования. Обычно рабочие формулы метода сводятся в специальные таблицы, которые приводятся в литературе. Так, для кратной двухфакторной модели вида z = x/y применяются следующие формулы интегрального метода:
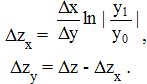
Логарифмический метод применяется для измерения влияния факторов в мультипликативной модели. Как и при интегрировании, здесь результат расчета также не зависит от месторасположения факторов в модели. По сравнению с интегральным методом логарифмический обеспечивает более высокую точность расчетов. Если при интегрировании дополнительный прирост (т.е. неразложимый остаток) распределяется поровну между факторами, то с помощью логарифмирования результат совместного действия факторов распределяется пропорционально доли изолированного влияния каждого фактора на уровень результативного показателя. В этом преимущество метода, недостаток – ограниченность применения. В логарифмическом методе также применяются свои рабочие формулы, однако здесь используются не абсолютные приросты показателей, а индексы их роста (снижения). Для модели z = xy используются следующие формулы логарифмического метода:
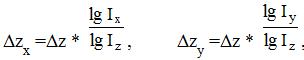
где символом I обозначается индекс – отношение фактического значения за отчетный период к значению базисного периода:
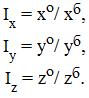
Читать дальше:
#a href="http://www.systematy.ru/articles/53_metodyi_kompleksnoy_otsenki_hozyaystvenno-finansovoy_deyatelnosti">#5.3. Методы комплексной оценки хозяйственно-финансовой деятельности#/a#
Похожие статьи:
| 1.3. Управление в организационно-экономических системах |
| 28 марта 2012, |
| 1.3. Управление в организационно-экономических системах Система управления предприятием является иерархической системой, в которой выделяются различные уровни управления (рис. ... Читать полностью |
| 5.1. Предмет, задачи, способы и приемы экономического анализа |
| 29 марта 2012, |
| 5.1. Предмет, задачи, способы и приемы экономического анализа Развитие и приложение методов анализа систем к экономическим задачам, задачам управления предприятиями (организациями) привело к п ... Читать полностью |
| Тема 2. Информация в экономических информационных системах. Количество информации. Методы оценки ч.2 |
| 07 мая 2012, |
| Семантический подход очень трудно формализуем, возможным путем является следующий. Используется тезаурусная мера. Если есть тезаурус S потребителя – отражает знания его о данном предмете ... Читать полностью |
| Тема 1. Информация в экономических информационных системах Управление в организационно-экономических системах ч.2 |
| 06 мая 2012, |
| На рис.1.3. используются следующие обозначения: УС – управляющая система; СУ – субъект управления (говорят также «управляющий орган»); ИО – исполнительный (исполняющий ... Читать полностью |
| 1.4. Адаптивные системы |
| 28 марта 2012, |
| 1.4. Адаптивные системы С такими терминами, как «управление» и «система управления» тесно связывается понятие адаптивных систем. Термин адаптация в общем случае подр ... Читать полностью |