3.4 Байесова модель. ч.2
В конкретных задачах для ЭС можно определить больше причин, чем две. Поэтому рассмотрим формулу Байеса для случая, когда предполагается n несовместных событий, составляющих полную группу:
P(Hi/A) = { P(Hi) P(A /Hi) } / {P(H1) P(A /H2)+ P(H2) P(A /H2)+…+
+ P(Hi) P(A /Hi) + …+ P(Hn) P(A /Hn)},
или
P(Hi/A) = P(Hi) P(A /Hi) / ∑ P(Hi) P(A /Hi)
где P(Hi/A) – апостериорная вероятность события Hi после наблюдения А.
Отметим, что если кроме двух точных причин Н1, Н2 не удается назвать другие, можно использовать формулировку «другие причины» - Н3, как мы и делали выше.
В диагностической системе взаимосвязь между разными событиями может быть более сложная - многоуровневая, как на рис. 3.2.
Связи на этом рисунке означают, что, например, событие H1 также есть результат возможных причин – E1 и E2, т.е.:
P(H1) = Р(E1)Р(H1/E1) + Р(E2)Р(H1/E2).
Тогда диагностика причин происходит в два этапа. На первом этапе вычисляются апостериорные вероятности причин - событий А:
P(H1/A) = P(H1) P(A /H1) / [ P(H1) P(A /H1) + P(H2) P(A /H2)].
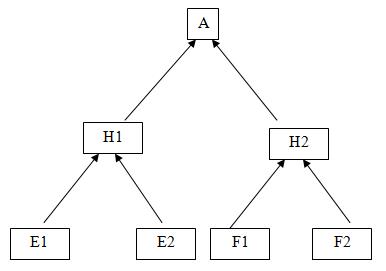
Рис.3.2. Граф связей между событием А и его причинами
Обозначим р= P(H1/A). Далее по формуле Байеса находятся вероятности P(E1/H1) и P(E2/H1). Учтем, что в данном случае однозначной уверенности в возникновении Н1 нет, то есть событие-причина Н1 произошло с вероятностью p. Отсюда и вероятность того, что Е1 или Е2 стали причинами для А вычисляется с учетом р:
Р(Е1/А) = P(E1/H1)*р, Р(Е2/А) = P(E2/H2)*р.
Таким образом, вычисляя все вероятности событий – вершин на графе и доходя до нижнего уровня, можно вычислить все вероятности всех возможных причин. Дальнейшие действия системы могут быть разнообразны – пользователь может получить упорядоченный список причин; возможно подключение нового сегмента знаний для дальнейшего уточнения вероятностей иным способом или предоставление сведений о способах действий при тех или иных причинах.
Существенным недостатком способа представления знаний на основе формулы Байеса является то, что необходимо заложить в систему много информации об априорных и условных вероятностях. Это трудоемко тем более, чем более сложной является задача. В этом случае еще более разнообразен граф связей в БЗ (см. рис. 3.2), который может расти как за счет уровней, так и за счет числа событий на верхних уровнях.
Значения априорных и условных вероятностей могут вычисляться на основе статистических сведений, или это могут быть экспертные оценки вероятностей. В последнем случае говорят о субъективной вероятности событий.
Читать дальше:
Похожие статьи:
| 3.4 Байесова модель. ч.1 |
| 11 июля 2012, |
| Эта модель может рассматриваться как та же модель продукций, но основанная на несколько ином понятийном аппарате. Фактически формула Байеса дает нам еще один способ для представления и об ... Читать полностью |
| 3.3 Представление и обработка неопределенности в продукционных системах |
| 11 июля 2012, |
| В реальных условиях далеко не всегда эксперт может с полной уверенностью сказать, что «Если А, То B». Скорее всего при работе вместе с инженером по знаниям над заполнением&nbs ... Читать полностью |
| Тема 4. Информационное моделирование предметной области при построении ЭИС. Понятие и содержание жизненного цикла ЭИС. ч.4 |
| 01 июня 2012, |
| На уровне концептуального моделирования выделяются основные понятия ПО и взаимосвязи между ними. В результате формируется наименее формализованное представление ПО, которое пока не связывается с са ... Читать полностью |
| Тема 4. Информационное моделирования при построении ИПС. Информационное моделирование при построении АСУ. ч.2 |
| 02 июня 2012, |
| При построении и внедрении АСУ на предприятии на этапах обследования и оптимизации бизнес-процессов (подробнее про этапы – см. тему 5) строятся две информационные модели (рис.4.7): ... Читать полностью |
| 3.3. Функциональные и структурные математические модели |
| 28 марта 2012, |
| 3.3. Функциональные и структурные математические модели Математическая модель, записанная в виде (3.5), (3.6) или (3.7), т.е. с помощью выражений, показывающих выходные реакции системы на вход ... Читать полностью |