3.4.Оптимизационные математические модели

3.4.Оптимизационные математические модели

Среди широкого круга задач, решаемых с помощью функциональных математических моделей можно выделить два основных их вида: задачи прямого счета и оптимизационные задачи. К первым относят такие задачи, в которых результат получают подстановкой исходных данных в заданную формулу (систему уравнения, неравенств). Математические модели, предназначенные для таких задач, показывают реакцию системы в ответ на некоторые исходные данные – параметры состояния и (или) входные воздействия.

В оптимизационных задачах ставится иная цель – определить некоторое желаемое (максимальное или минимальное) значение целевой функции путем подбора соответствующих значений входных переменных.

Обобщенная оптимизационная модель запишется следующим образом:

y = f(X) ® max (min)

gj(X) <= bj, j = 1, 2, 3, ..., m,

где y – выходная характеристика (критерий оптимизации), которую требуется привести к экстремальному значению – максимуму или минимуму в зависимости от ее смысла;

f(X) - целевая функция, т.е. функция, указывающая зависимость критерия оптимизации от значения параметров Х;

X = (x1, x2, x3, ..., xn ) - набор из n параметров процесса, которыми можно управлять при поиске (создании) оптимального решения, эти параметры процесса называют в теории оптимизации переменными процесса, а Х - вектором состояния процесса; еще говорят, что х есть компоненты (координаты) вектора Х;

gj(X) - функции-ограничения, число которых равно m;

bj - некоторые постоянные величины выражающие количественные значения ограничений;

«<=» - знаки «меньше или равно», в записи ограничения вместо этого может быть и «меньше», «больше или равно», «больше», а также «равно».

В зависимости от вида функций f(X), gj(X) различают такие известные модели, как модели задач линейного, нелинейного, целочисленного программирования и др.

Оптимизационные модели находят широкое применение в системном анализе, исследовании операций для поиска и количественного обоснования оптимальных решений, особенно, в экономических, социальных, организационных системах.

Например, оптимизационная модель задачи линейного программирования может использоваться для оптимального планирования выпуска продукции предприятия. Пусть предприятие может выпускать n видов продукции. Требуется определить, сколько единиц того или иного вида продукции следует произвести в заданный период, чтобы при этом получить максимальную прибыль и уложиться в имеющиеся ограничения на ресурсы (материальные, финансовые, кадровые и др.). Обозначим xi – число единиц продукции i-го вида; aji – затраты j-го ресурса на выпуск единицы i-ой продукции; bj – имеющийся запас j-го ресурса; ci – прибыль от реализации единицы i-й продукции. При этих обозначениях можно записать следующую модель в виде классической задачи линейного программирования:

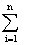cixi ® max,

ajixi <= bj , j = 1, 2, 3, ..., m,

xi => 0, i = 1, 2, 3, ..., n.

Решением данной задачи будет вектор X* = (x1*, x2*, x3*, ..., xn* ), в котором компоненты xi* (некоторые из них могут быть равны нулю) показывают, сколько единиц i-й продукции нужно выпустить, чтобы прибыль при данных ресурсах была наибольшей.

Читать дальше:

#a href="http://www.systematy.ru/articles/35_imitatsionnoe_modelirovanie"#3.5. Имитационное моделирование#/a#