3.2 Продукционная модель (правила продукций). ч.1
Продукционная модель представления знаний является, пожалуй, наиболее распространенной в ИИС. В общем виде правило продукций записывается так:
Если <Условие> То <Заключение>,
где <Условие> может представлять из себя сложное высказывание, состоящее из более простых, связанных связками “И” , “ИЛИ”, “Не”.
В более лаконичном виде пишут еще так:
А → B,
где А – в общем случае сложное условие, а B –... Подробнее
3.2 Продукционная модель (правила продукций). ч.2
При формализации этих знаний они будут преобразованы в более строгую форму вида А → B, где однозначно определяется факт А, и левая часть правила трактуется как утверждение об истинности или ложности А. Так вместо размытого выражения «приближаются праздничные дни» в правиле может фигурировать более конкретное:
Если Праздничные дни = Скоро, То Ожидаемые продажи напитка С = Возрастают,
где термины «Скоро» , «Возрастают» являются элементами... Подробнее
3.2 Продукционная модель (правила продукций). ч.3
В работе машины вывода ЭС могут использоваться две стратегии вывода:
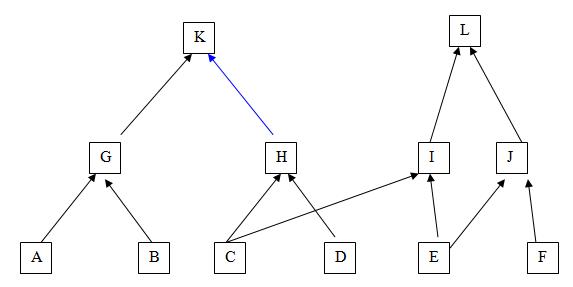
- прямая стратегия вывода. В этом случае вывод осуществляется то данных (снизу вверх на рис.3.1), т.е. сначала у пользователя запрашиваются сведения о фактах A,B, C и т.д. После получения нужных сведений проверяется истинность фактов G,H… . Далее выполняется переход к проверке конечно (на данном рис.3.1.) гипотезы K;
- обратная стратегия вывода. В этом случае движение по дереву осуществляется сверху вниз. То... Подробнее
3.3 Представление и обработка неопределенности в продукционных системах
В реальных условиях далеко не всегда эксперт может с полной уверенностью сказать, что «Если А, То B». Скорее всего при работе вместе с инженером по знаниям над заполнением БЗ эксперт будет говорить о какой то возможности того, что «Если А, То В».
Точно также, как и в ходе диалога пользователя с системой на вопрос об истинности факта А он не всегда сможет однозначно ответить «истинно» или «ложно».
Для того, чтобы... Подробнее
3.4 Байесова модель. ч.1
Эта модель может рассматриваться как та же модель продукций, но основанная на несколько ином понятийном аппарате. Фактически формула Байеса дает нам еще один способ для представления и обработки неопределенности в продукционных системах.
Разрабатывая вместе с экспертом концептуальную модель предметной области, инженер по знаниям может увидеть, что эта ПО хорошо описывается в терминах событий, вероятностей событий, а также причинно-следственных взаимосвязей между ними.
Например,... Подробнее
3.4 Байесова модель. ч.2
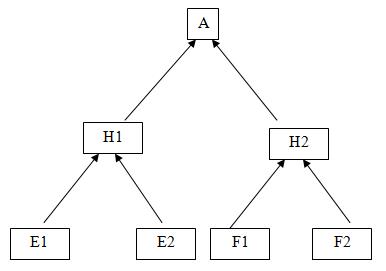
В конкретных задачах для ЭС можно определить больше причин, чем две. Поэтому рассмотрим формулу Байеса для случая, когда предполагается n несовместных событий, составляющих полную группу:
P(Hi/A) = { P(Hi) P(A /Hi) } / {P(H1) P(A /H2)+ P(H2) P(A /H2)+…+
+ P(Hi) P(A /Hi) + …+ P(Hn) P(A /Hn)},
или
P(Hi/A) = P(Hi) P(A /Hi) / ∑ P(Hi) P(A /Hi)
где P(Hi/A) – апостериорная вероятность события Hi после наблюдения А.
Отметим, что... Подробнее
3.5 Сетевые модели и графы. ч.1
Математическая сеть представляет собой множество объектов и взаимосвязей между ними. Объекты в сети отображаются вершинами (горят еще – узлами сети), а взаимосвязи между ними – ребрами или ветвями сети (если они неориентированы) или дугами (если взаимосвязь ориентированная, однонаправленная).
Частным случаем сетевой модели являются обычные бинарные графы, которые могут быть ориентированными или неориентированными. Граф математически задается в виде набора элементов:
(X,V,... Подробнее
3.5 Сетевые модели и графы. ч.2
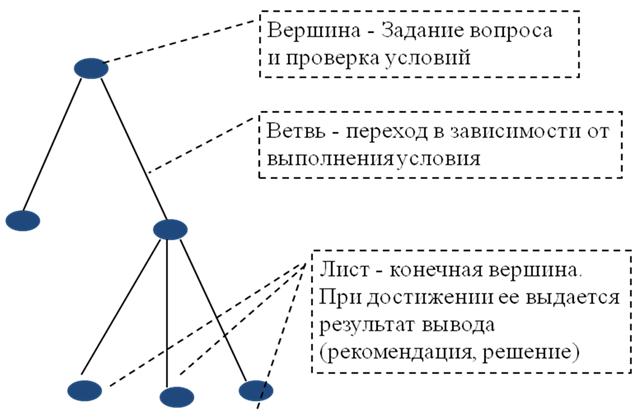
Еще одним примером графовой модели знаний может служить так называемое дерево решений (дерево – это вид графа, в котором нет циклов). В дереве решений (рис.3.3) может быть заложен процесс вывода результата – решения некоторой задачи, который состоит в последовательной проверке каких-то условий (например, путем выдачи пользователю вопросов относительно значения того или иного параметра).
Рис.3.3 – Дерево решений
Дерево решения может... Подробнее
3.5 Сетевые модели и графы. ч.3
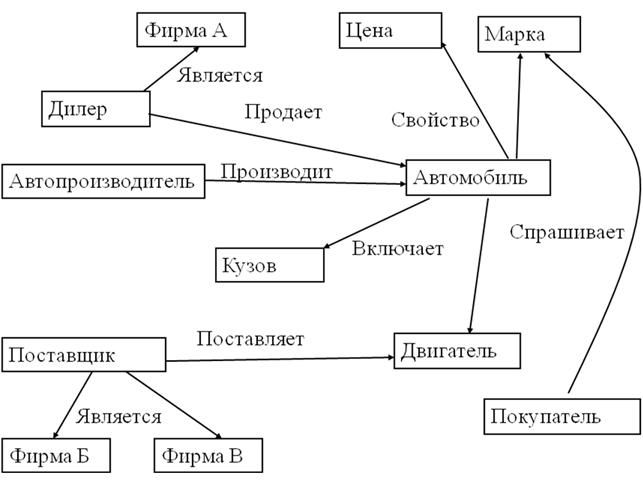
Вершины в семантической сети (СС) могут означать разные по природе объекты, а дуги между ними – различные по смыслу отношения. Это позволяет строить сложные и полные модели предметной области, с достаточной степенью подробности воспроизводящие объекты и их взаимосвязи.
На рис.3.5. приведен иллюстративный пример семантической сети, в которой показаны знания о разных объектах предметной области: знания об автомобилях и их свойствах, знания о составных частях автомобиля, знания о... Подробнее
3.6 Рейтинговая модель
Идея этой модели представления знаний и вывода решений базируется так же на идее диалога с пользователем, когда пользователю задаются вопросы и, возможно, предлагаются варианты ответов.
Таки образом, как и в дереве решений знаниями эксперта будут эти самые вопросы и варианты ответов. Однако, на этом сходство заканчивается.
Пусть имеются гипотезы G1, G2, G3, а работа системы состоит в сборе свидетельств в пользу этих гипотез. Будем говорить, что в ходе вывода строится рейтинг... Подробнее
Аннотации статей | [Все аннотации] |
|
|
|||||
|
|
Рекомендовано:
 Робот - мойщик окон
Это, на самом деле, крутая штука
Робот - мойщик окон
Это, на самом деле, крутая штука ЗДЕСЬ
Популярные статьи |



